With large amounts of investment fuelling research and development of scalable blockchain technologies, the next decade is likely to see a rapid growth in its mainstream adoption. However, among the many barriers to its widespread use is the concern of quantum computing (QC) advances and its possible impacts on the security of blockchain technology. In this article we explain current vulnerabilities of blockchain, as well as indicate possible solutions.

Contents:

FAQ
Introduction
Current Vulnerabilities
Post-Quantum Cryptography
  Hash-Based Cryptography
  Multivariate Cryptography
  Code-Based Cryptography
  Lattice-Based Cryptography
Quantum Cryptography
Appendix
References

FAQ

What is Shor’s Algorithm?

Proposed by Peter Shor as a solution to the prime factor problem to be implemented in a quantum computational environment, Shor’s Algorithm indicates that cryptography based on this problem will not work in such an environment. Given an ideal quantum computer using Shor’s Algorithm a user could find the prime factors of a number in polynomial time. As RSA encryption relies on the property that prime factors can be generated in exponentially less time than they can be found given their multiple this public-key infrastructure would become unsustainable.

What is Grover’s Algorithm?

In a classical computational environment no algorithm has been resolved that allows a user to search for an object out of $n$ objects without checking each object one-by-one. However, Grover’s Algorithm can be implemented on a quantum computer to allow for a user to search through an unordered set of objects and find their required object in a number of iterations that is the square of the total number of objects, instead of being equal to the total number of objects. One of the clearest applications of this algorithm is to the case of hash functions, where a collision between two inputs giving the same output can be found in significantly fewer steps than possible otherwise. In addition to the birthday paradox it could be said that using Grover’s Algorithm would allow a user to find any collision (rather than a specific collision) in the cubic root number of steps than would have otherwise been required.

What cryptographic schemes are vulnerable to quantum computation?

There are many cryptographic primitives in use today that are vulnerable to efficient quantum algorithms. Shor’s Algorithm for instance ensures that any cryptography that relies on the difficulty of the prime factors problem can be solved efficiently by any quantum malicious actor. Elliptic Curve Cryptography and almost all other schemes that are intended to provided their users confidentiality (i.e. public-key infrastructures) are vulnerable as well. In fact the only commonly used scheme for network messaging that is not completely vulnerable to quantum computation is hash functions - as long as a high enough security level is used (i.e. 512 bits).

Why are quantum computers consequential to blockchain?

Blockchain networks rely heavily on public-key infrastructure and the existence of other cryptographic primitives that can guarantee integrity. While hash functions are capable of verifying the origins of a message, on their own without schemes that can provide confidentiality there is no feasible hash function (one that isn’t computationally prohibitive) that as such guarantees integrity. Without integrity it is possible for any malicious actor to spend funds from another actor’s account without their consent as no one can be sure who the genuine actor is. Quantum computation and the implementation of efficient algorithms such as Shor’s Algorithm makes any known confidentiality schemes infeasible to implement, meaning blockchain networks would not be able to operate as they do now. Only new schemes that are safe against quantum computation can guarantee the post-quantum future of blockchain networks.

What is a One-Time Signature?

One-Time Signatures are schemes derived from the field of hash-based cryptography that allow for integrity of messages sent over a network even where confidentiality does not exist. ‘One-Time’ refers to the notion that all signatures of this type can only be used once before they are vulnerable to being exploited to forge signatures for new messages. Therefore, each time a user desires to prove the integrity of their message with a One-Time Signature they must generate a completely new signature with a new public key. It is this element that make them computationally prohibitive to implement, as each single message requires significant computation and/or proof sizes. There are two commonly proposed varieties of One-Time Signatures: Lamport Signatures, and Winternitz Signatures.

What is a Few-Time Signature?

Using Merkle Trees it is possible to concatenate $n$ One-Time Signatures that a user has generated into a single public key. By sharing this public key with other users, the sender of messages can use up to $n$ individual One-Time Signatures to sign a single message each without risk of their signature being forged. Therefore, the sender is able to perform all necessary computation before sending a collection of messages and does not need to share a new public key each time. However, while there are advantages to this extent, there are also disadvantages in that more computation must be performed and that proof sizes do increase.

How is Code-Based cryptography used?

Any schemes derived from the field of code-based cryptography relies on the concept common to many other schemes, encryption and decryption. However, these operations are performed in a different manner. To ‘encrypt’ a message the sender will introduce errors to said message (errors are the flipping of bits or bytes) before sending it across the network where it will appear as unintelligible to any eavesdroppers. The recipient of the message will have to ‘decrypt’ the message by applying some function to the message that removes the introduced errors and aggregates said message to a form that is valid.

How is Multi-Variate cryptography used?

Multi-Variate cryptography relies on the difficulty of solving $m$ quadratic polynomials over a finite field, where solving in this case means that for each polynomial they must be equal to zero. In other words, any malicious actor attempting to forge a signature would need to find the secret object $x$ such that all polynomials are equal to zero. The set of polynomials, as well as details about the map said polynomials are generated across, are included together as the public-key that must be shared. However, this does tend to mean signature sizes are computationally prohibitive for the purposes of encrypting messages.

How is Hash-Based cryptography used?

Relying on the provably hard problem of finding the inverse or a collision for any given output, hash functions can be used to generate schemes for confidentiality and integrity in network communications. The use of hash functions, either in chains or other patterns, forms the basis for hash-based cryptography. Even with quantum computation available it has been proven that Grover’s Algorithm would not make hash functions unviable to use (as long as their security level was doubled). However, hash-based cryptography is characterised by One-Time Signatures (that can only be used once before being vulnerable), and Few-Time Signatures (that can only be used a finite number of times); both of which require large amounts of computation and large proofs for a single message.

Introduction

The vulnerability of blockchain technology to the rapid development of QC has been a significant area of concern in the blockchain development community. With proposals for quantum resistant protocols, in recent years there has been a notable push towards constructing systems that take into account a possible quantum future.

In Section 2 we explore current vulnerabilities of blockchain technology to quantum attacks, before reviewing the various solutions in Section 3. Finally, Section 4 will introduce the possible inclusion of quantum cryptography to mitigate the problems that quantum computing itself brings. It should be noted that this article assumes no prior knowledge of quantum computing and is mainly catered for those in the blockchain community. Therefore, before we delve into the aim of the article, we supply a brief overview of the expanding field of quantum computation. This can serve as an introduction to those that have never come across the term and are puzzled when hearing this new form of computation.

Quantum computation

The concept of a computational device that employs quantum mechanics was in fact suggested before the advent of modern day classical computers. The realisation of QC was limited, not by algorithms that in situations promised exponential speed-up over classical computers, but rather the engineering required to construct the fragile qubits required. Qubits are the basic units for quantum information and are analogous to classical bits. There are many ways to engineer a qubit, ranging from employing superconducting semiconductor circuits (used by firms such as Google and IBM), to the manipulation of individual ions (used by firms such as IonQ). Though there are many implementations of the qubit, it is an object that behaves quantum mechanically, allowing one to exploit the exotic behaviour that exists only in the realm of quantum physics. Qubits are clearly crucial, which then raise questions of:

  1. How they behave;
  2. How we can write them down mathematically, and;
  3. How they allow for a distinct form of computation.

As opposed to the binary 0 or 1 states stored in bits, qubits can be in a probabilistic combination of 0 and 1 represented as a vector $[p_0,p_1]^T$, where $p_0$ and $p_1$ are the probabilities of being in state 0 and 1 respectively. This is known as being in a superposition of the two states 0 and 1. However, $p_0$ and $p_1$are not entirely probabilities as $p1, p2 \in \mathbb{C}$. To get even weirder, systems of these qubits can become entangled, resulting in qubit states that are correlated. For example, the addition of a qubit gives a probabilistic superposition of the four combinations $[00, \ 01, \ 10, \ 11]$, which doubles the floating point numbers required to determine the combined quantum state, $[p_0,p_1, p_2, p_3]^T$. Another way to understand the profoundness of this is by comparing this with vectors or arrays in memory. The addition of a space in memory increases the vector dimension, and hence the degree of freedom, by one. This is in contrast to quantum computers, where the addition of a single qubit doubles the dimension of the vector that represents it (i.e. the degrees of freedom grows exponentially with the number of qubits). This is why it is in general impossible to simulate large quantum systems. The superposition of inputs will become important later when we will see that we are able to evaluate functions in superposition (i.e. in parallel).

Many of the details discussed so far are not necessarily crucial to comprehend the implications of quantum technology. They have been stated so that it is not entirely unintelligible where exactly the advantage arises from using quantum computers. On the other hand, if there is anything observed from this brief QC introduction, it should be the existence of two algorithms that have major implications on the cryptographic techniques underlying most blockchain technologies: Shor's Algorithm and Grover's Algorithm.

Shor’s Algorithm

Perhaps the most significant or widely known quantum algorithm, Shor’s Algorithm was proposed by Peter Shor in 1994 [12]. Running in polynomial time on a quantum computer, instead of exponential time on a classical computer, this algorithm is capable of solving the integer factorisation problem. Adapting the factoring problem into finding the period of a function. Say we want to factorise a semi-prime integer $N=15$, we observe the following function:

$$ \begin{equation*} f(k)=a^k \ \mathrm{mod} \ N \end{equation*} $$

Choosing random $a=2$, we can compute: $f(0)=1, \ f(1)=2, \ f(2)=4, \ f(3)=8, \ f(4)=1$ and observe that there is in fact a periodicity to the function $f$. More specifically we see that $f(k)=f(k+r)$ where $r=4$ in the case of $a=2$ above. $r$ is often referred to as the period of the function. Assuming that we have a way to find this period we have the following, where $k$ is an integer greater than 0.

$$ \begin{align*} 1&=f(r)=a^r \ \mathrm{mod} \ N \\ 0&=a^r-1 \ \mathrm{mod} \ N \\ 0&=(a^{\frac{r}{2}}+1)(a^{\frac{r}{2}}-1) \ \mathrm{mod} \ N \\kN&= (a^{\frac{r}{2}}+1)(a^{\frac{r}{2}}-1) \end{align*} $$

The last step occurs because $0 \ \mathrm{mod} \ N$ implies the terms $(a^{\frac{r}{2}}+1), \ (a^{\frac{r}{2}}-1)$ must be factors of a multiple of $N$. We still need to compute the exact multiple, however this can be performed using the efficient Euclidean algorithm for computing the greatest common divisor (GCD). Computing $GCD(a^{\frac{r}{2}}+1, \ N)$ and $GCD(a^{\frac{r}{2}}-1, \ N)$ will necessarily give a non-trivial factor of $N$. If we obtain an odd $r$ or if the factors are trivial we repeat the process for a different a which will give a different $r$. Therefore, if we have an efficient way to find the period of $f(k)$, we have an efficient way of factoring any integer $N$.

Classically there is no efficient way to compute the period of such a function. However, with a quantum device one is able to find the period in $\text{poly}(\log{(N)})$ which is exponentially faster. This is done with what is known as the Quantum Fourier Transform (QFT); analogous to the Discrete Fourier Transform (DFT). A Fourier transform decomposes a function into its frequency composition and is used in fields ranging from signal processing to physics. Clearly, having such a decomposition will allow us to compute the period of the function $f$, which has an inverse relation to the frequency found with a DFT. Fortunately for encryptions schemes like RSA, computing the DFT is infeasible and its complexity grows exponentially with the number of bits. The most efficient method of computing the DFT is the Fast Fourier Transform (FFT) which has a complexity $O(n2^n)$ where $n$ is the number of bits. However, performing this decomposition is efficient using the QFT on a quantum computer with complexity $O(n^2)$. It is this that allows Shor’s algorithm to break encryption protocols based on the hardness of factorisation. What would be practically impossible on a classical computer, a quantum computer is predicted to factor a 2048 bit number in about 8 hours [13].

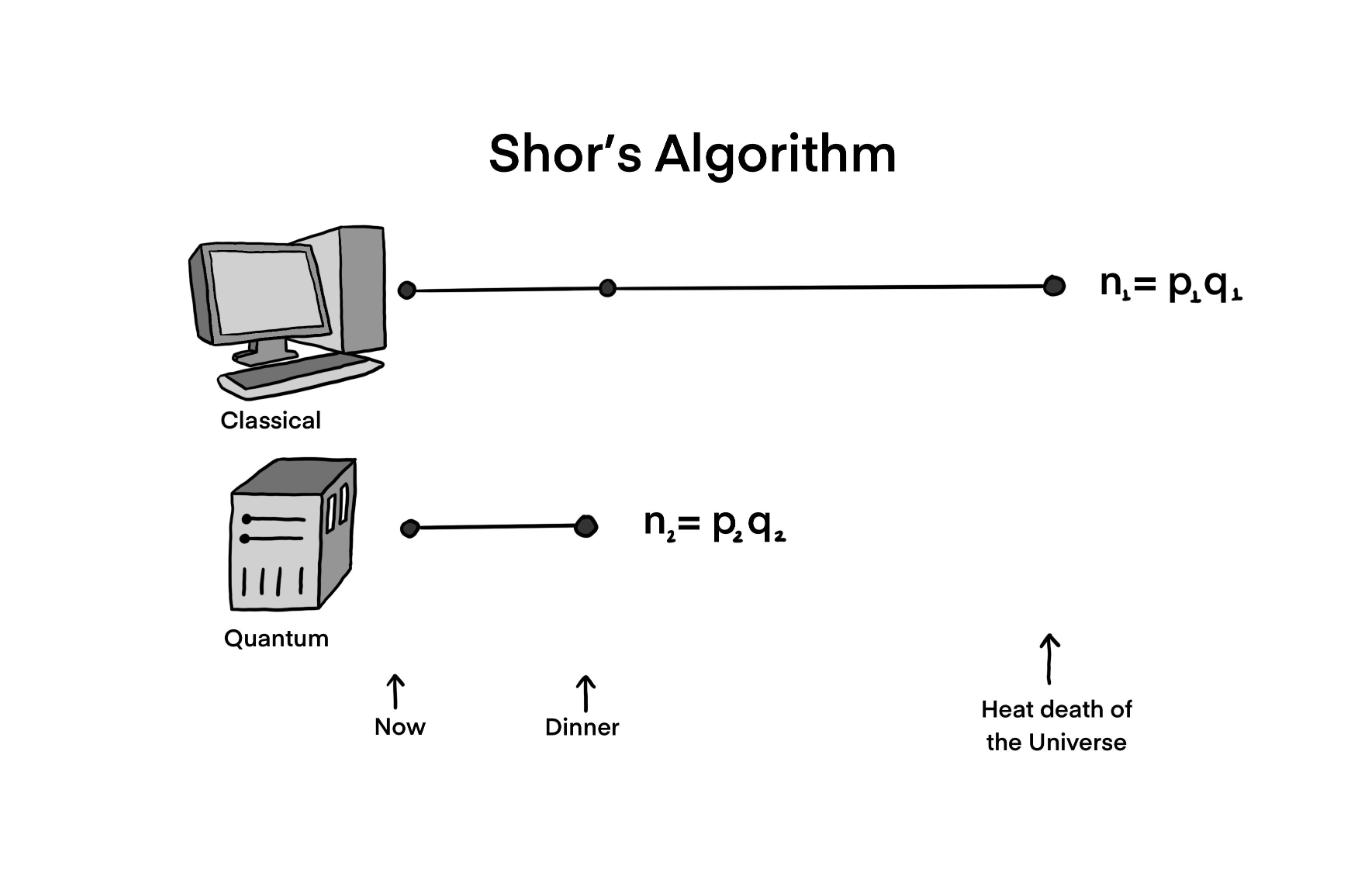
Simplified depiction of the exponential speed-up quantum computers provide for prime factorisation. Simplified depiction of the exponential speed-up quantum computers provide for prime factorisation.

Generalising Shor’s algorithm we see that a quantum computer is able to efficiently solve the hidden subgroup problem over a finite Abelian (i.e. where the binary operation is commutative $a\cdot b=b\cdot a$) group. This enables the efficient solving of the Discrete Logarithm Problem problem with a quantum computer. Being able to efficiently solve DLP will also enable quantum computers to break elliptic curve cryptography which secures blockchains such as Bitcoin and Ethereum.

Discrete logarithm problem. Given a finite Abelian group $G$ with binary operation $\cdot$ and $a^m:=\Pi_i a$ , the discrete log problem (DLP) requires one to find $k \in \mathbb{Z}$ that solves:

$$ \begin{equation*} \exists a, \ b \in G : b^k=a \end{equation*} $$

Grover’s Algorithm

Grover’s algorithm is an unordered search algorithm that provides a quadratic speed-up to the best classical method. This may seem highly counterintuitive when one thinks about the problem we are trying to solve. Say we are trying to find a particular number given an array of size $N$, it seems impossible to do better than iterating through the array element by element giving a complexity of $O(N)$. However, we will see that Grover’s algorithm allows us to do this in a complexity of $O(N)$; seemingly against common sense.

We will walk through the algorithm at a high level, which will allow one to have an understanding of the algorithm without requiring a background in quantum information theory. The problem of finding an element in an unordered list is directly equivalent to the problem of finding $x$ such that $g(x)=1$ where $g : X \rightarrow [0,1]$ with output $1$ for the marked state that is being attempted to be found, and $0$ otherwise.

Grover’s algorithm is depicted in in the below diagram at a high level which will be explored in greater depth through this section. The algorithm starts with a superposition of all possible inputs $X$ with an equal probability. This is a single quantum state over many qubits. The state is then passed through what is known as an oracle (note this is distinct to oracles in the context of blockchain). Here the oracle marks the state of interest (i.e. $g(x)=1$). This is then followed by an amplification operation that increases the probability of measuring the marked state. The oracle and amplification operations together are referred to as a Grover Iteration. The algorithm consists of multiple Grover iterations, maximising the probability of measuring the wanted state on the quantum computer. We finally measure the state which will most likely return the state that we are trying to find. It turns out that this algorithm has a complexity of $O(N)$ where $N=|X|$. Therefore, quadratically faster than iterating through the possible $x \in X$. It will be observed in ensuing sections that this allows for a possible speedup on the mining of blocks in Proof of Work-based blockchains. The task then becomes implementing the specific oracle on a quantum computer.

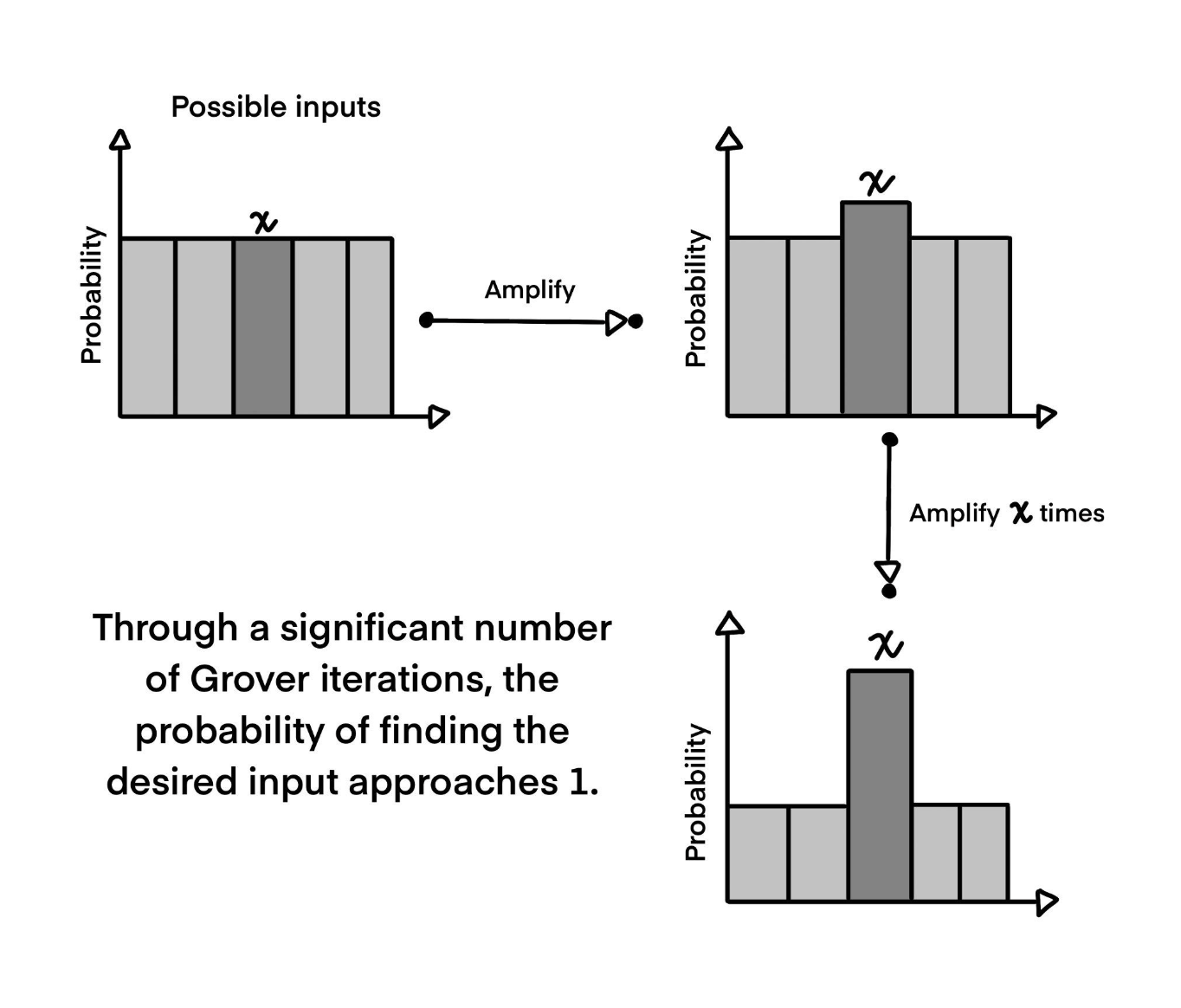High level illustration of Grover’s algorithm with $n$ Grover iterations. High level illustration of Grover’s algorithm with $n$ Grover iterations.

Current vulnerabilities

Most blockchain technologies contain a few vulnerable points of attack by a quantum computer. Two main concerns will be addressed: authentication and the mining process used for the Proof-of-Work consensus mechanism. They each suffer from Shor’s Algorithm and Grover’s Algorithm respectively with the former vulnerability by far a greater threat.

Authentication

One of the most commonly used cryptographic techniques used for authenticating user's transactions in blockchain is the Elliptic Curve Digital Signature Algorithm. Though it will soon be seen that it is susceptible to quantum attacks, it is useful to first understand its inner workings.

Elliptic Curve Digital Signature Algorithm

The Elliptic Curve Digital Signature Algorithm (ECDSA) achieves the same level of security with a smaller signature when compared to the most commonly used RSA algorithm. This scheme is based on the hardness of the elliptic curve discrete logarithm (ECDLP) problem. To understand this, an introduction to elliptic curves is stated. Elliptic curves are sets of points which, crucially, can be used to form a group structure. Visualisation of elliptic curves are possible in the below figure, where the existence of group law for elliptic curves are also presented. Where $\Delta = 4a^3+27b^2$ is the discriminant, with the requirement $\Delta \neq 0$ ensuring that the curve is non-singular, these curves have the form:

$$ \begin{equation*} E=(x, \ y) \in \mathbb{R}^2 : y^2=x^3+ax +b, \ \Delta \neq 0 \cup 0 \end{equation*} $$

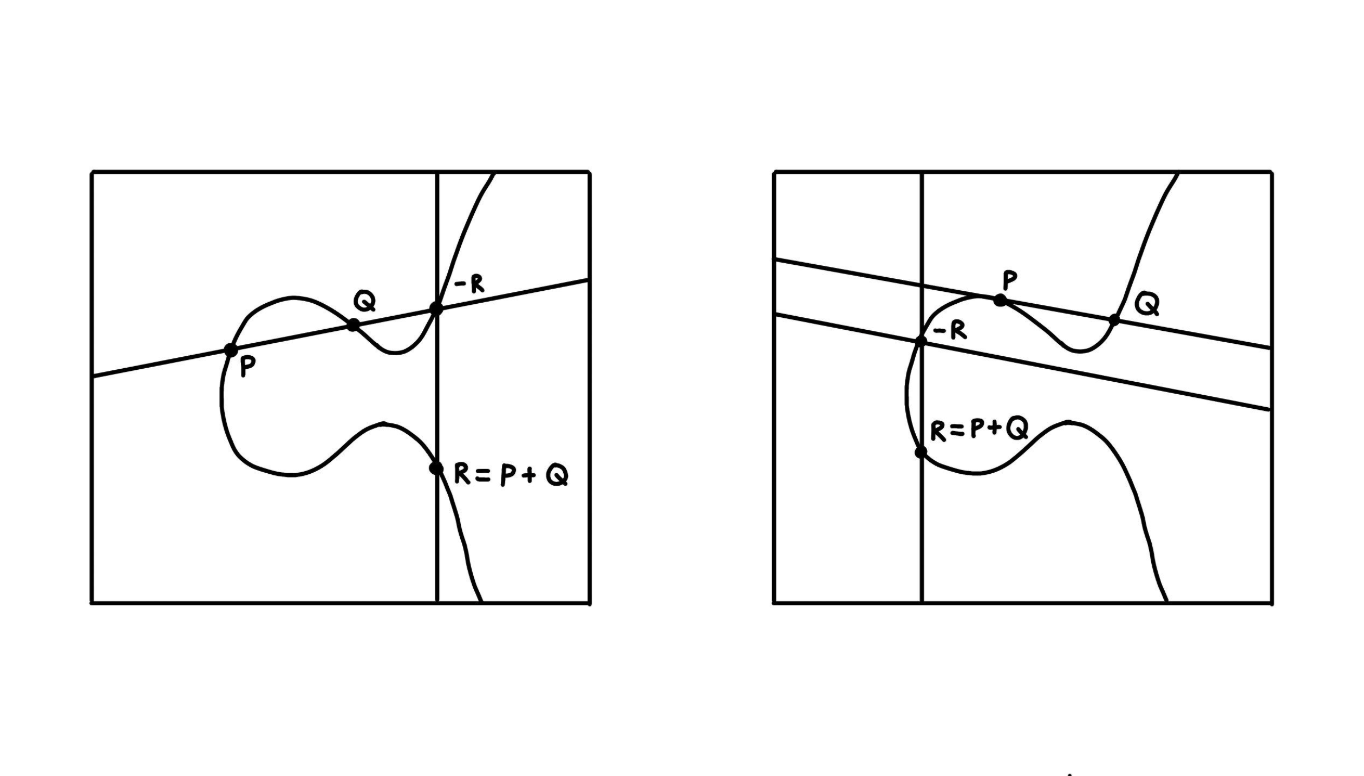
Two examples of elliptic curves depicted as a group under the notion of "group law". Two examples of elliptic curves depicted as a group under the notion of "group law".

We initially claimed that points on an elliptic curve can be treated as a group. Groups in mathematics are sets of objects with a binary operation (i.e. addition) that satisfy certain axioms that can be found in Appendix A. Hence, to define a group from the points on an elliptic curve, there is a requirement to also define a binary operation. This is done geometrically, as seen in the figure above. Given two points $P, \ Q$ where $P\neq Q$, it is defined that $P+Q$ is the $x$-axis reflection of the third point that intersects the curve $E$ and the line going through $P$ and $Q$. In the case $P=Q$, the line is set to be the tangent of point $P$ on the curve. The intersection of the line with the curve $E$ is the $x$-axis reflection of the binary operation. Clearly, there are points $P$ and $Q$ for which a line does not intersect the curve again. For example, when $P, \ Q$ have the same $x$-coordinate, the vertical line generated does not geometrically intersect the curve. It is for this reason, the elliptic curve $E$ is defined with the additional object $0$ which is a point at infinity. As a further note, scalar multiplication is defined as repeated addition, i.e. $nP:=\sum_{i=1}^n P$. With this definition of $+$ one can show that $(E, \ +)$ in fact forms a group. However, this is not entirely what is used in cryptography. The curves defined here are over infinite field $\mathbb{R}$, whereas in ECDSA the elliptic curve is transformed to a finite field $\mathbb{F}_p$ with $p$ elements. Specifically the curve has the form denoted below where $a, \ b \in \mathbb{F}_p$.

$$ \begin{equation*} E_{\mathbb{F}} =(x,y) \in \mathbb{F}_p^2 : y^2=x^3+ax +b \ \mathrm{mod} \ p, \ \Delta \neq 0 \ \mathrm{mod} \ p \cup 0 \end{equation*} $$

Elliptic curves over finite fields still form a group, however, there is now cyclic behaviour that is introduced (i.e. given a point $P$ it can repeatedly be added onto itself and eventually cycle back to $P$). This can be easily understood when looking at integers in a finite field with the binary operation being addition (i.e. starting at $P=4$ in a finite field of size $p=10$ and subsequently adding $P$). Any example can also be generalised into a simple form as depicted below as well.

$$ \begin{align*} 4 \ \mathrm{mod} \ 10 &\xrightarrow{+P} 8 \ \mathrm{mod} \ 10 \\ 8 \ \mathrm{mod} \ 10 &\xrightarrow{+P} 2 \ \mathrm{mod} \ 10 \\ 2 \ \mathrm{mod} \ 10 &\xrightarrow{+P} 6 \ \mathrm{mod} \ 10 \\ 6 \ \mathrm{mod} \ 10 &\xrightarrow{+P} 0 \ \mathrm{mod} \ 10 \\ 0 \ \mathrm{mod} \ 10 &\xrightarrow{+P} 4 \ \mathrm{mod} \ 10 \end{align*} $$

$$ \begin{equation*} \exists n : nP \ \mathrm{mod} \ p = P \end{equation*} $$

It is seen that $n=5$ iterations resulted in a cycle back to the original $P=4$. Here $5$ is referred to as the order of $P$ as the order is dependent on $P$, e.g. $P=3$ has order $10$ for the above finite field. Clearly finding the order $r$ of a point $P$ is equivalent to finding the smallest $r$ such that $rP=0 \ \mathrm{mod} \ p$. Interestingly, we have created a sub-group $E'|_P =[P, \ 2P, \ ..., \ rP]$ with the size of the subset (order) being dependent on $P$. For the example of adding integers, finding $r$ is not very difficult. However for the group formed by points from elliptic curves and a prime $p$, finding $r$ for a given $P$ is an extremely hard problem. The ECDSA uses this hardness to create a signature scheme, with the problem known as the Elliptic Curve Discrete Logarithm Problem.

Elliptic Curve Discrete Logarithm Problem (ECDLP). Let $E$ be an elliptic curve defined on a finite field $\mathbb{F}_p$ with $S,T \in E$. ECDLP requires one to find an integer $r$ such that $T=rS$.

For classical computers this problem is exponentially hard to solve. However, ECDLP is precisely the discrete logarithm problem we observed (in Section 1.1.1) to be vulnerable to Shor’s algorithm. Through explaining ECDSA we will see that the ability of quantum computers to efficiently solve ECDLP will mean that this cryptographic scheme, which is used in a substantial number of blockchains, is not secure. Using all the presented knowledge it is now possible to understand how exactly ECDSA works looking at the protocol in three stages: key generation, signature generation and signature verification. As will be common throughout this article, it is assumed that Alice signs a message that will be verified by Bob.

Key Generation. Given a random elliptic curve, an associated base point $G$, prime modulus $p$, and order $r$ (all of which is public data), a random private-key $K_S \in [1, ... , r-1]$ is generated. The public-key is generated by computing $K_P=K_S G \ \mathrm{mod} \ p$. Note that given $K_P$ and $G$ the problem of solving for the private-key $K_P$ is the ECDLP that is equivalent to the discrete log problem.

Signature Generation. The message $m$ is first hashed and then truncated such that the bit-length of the hash is the same as the bit-length of $r$, giving a hash $z$. Alice chooses a random integer $k\in [1, ... , r-1]$ and the point $P=kG$ is computed. Alice then computes $d=x_P \ \mathrm{mod} \ r$ where $x_P$ is the $x$-coordinate of point $P$. Finally $s=k^{-1}(z+dK_P)$ is calculated, where $k^{-1}$ is the inverse of $k \ \mathrm{mod} \ r$. If either $d$ or $s$ is computed to be $0$ then Alice tries again with a different $k$. The signature is defined as the tuple, $S=(d, \ s)$ and is sent with the message $m$.

Signature Verification. To verify, Bob computes $u=s^{-1} z \ \mathrm{mod} \ r$ where Bob computes $z$ in the exact same way as done by Alice. Bob also computes $v=s^{-1}d \ \mathrm{mod} \ r$ to finally calculate $P=uB+vK_P$. The signature is deemed valid only if $d=x_P \ \mathrm{mod} \ r$.

The mathematical proof of why this signature generation/verification works is supplied in Appendix B. It is the public/private-key generation that leaves this scheme vulnerable to quantum computers. Given $K_P$ and $G$ a quantum computer is able to efficiently find $K_S$ meaning that the private-key is no longer private. This vulnerability requires one to employ quantum resistant cryptographic techniques, which will be discussed later.

Public-key cryptography

The primary form of public-key cryptography employed is RSA where a public-key/private-key pairing is generated through a reliance on multiplying large prime numbers. It can be immediately observed that while factorising a number into its two prime factors is computationally infeasible for a classical computer, Shor’s Algorithm is able to find these factors in polynomial time. An explanation of how exactly the keys used for RSA are generated is provided to indicate how more specifically Shor’s Algorithm does break this cryptography.

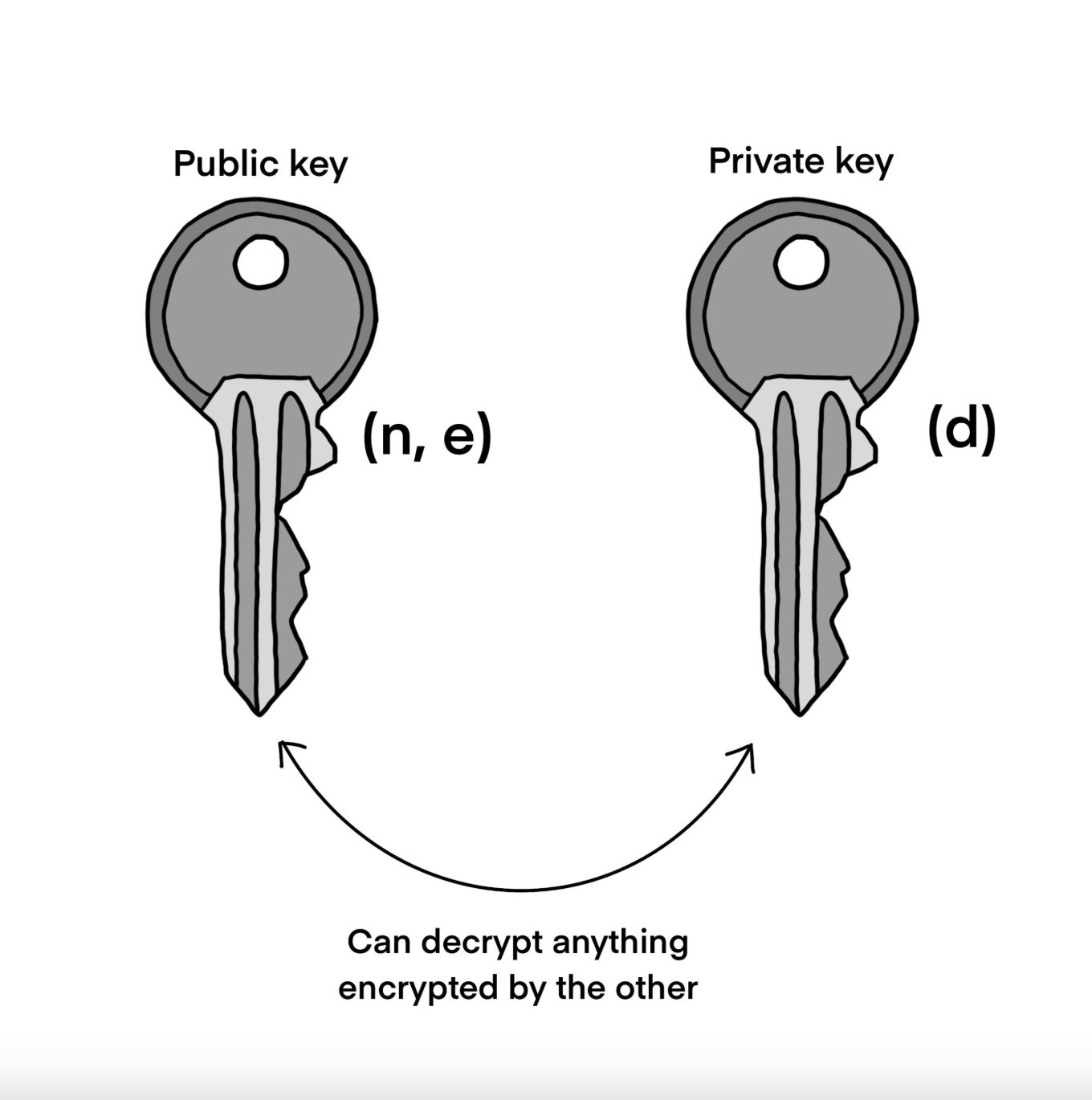Depiction of the interaction between the private and public-key in a key-pair generated for a public-key cryptographic system. Depiction of the interaction between the public-key and private-key in a key-pair generated for a public-key cryptographic system.

RSA is used for both confidentiality (encrypting and decrypting any message), and integrity (proving that a message did originate from the owner of a given key-pair) in current systems. The latter is provided by a cryptographic primitive known as a digital signature, in which the hash of a message is sent alongside the message (which has been encrypted with the sender’s private-key) and both these two components are encrypted together with the receiver’s public-key. In RSA only the owner of the private-key pair for the public-key used to encrypt some message can decrypt said message (ignoring the possibility of employing Shor’s Algorithm). Likewise only a user possessing the sender’s public-key can decrypt any message encrypted with the sender’s private-key (though it is assumed that everyone has access to the sender’s public-key by Kerchoff’s Principle). As such the receiver only can decrypt the message and the hash of the message and easily verify by hashing the message themselves to check that the two values match. If so, assuming that RSA is cryptographically secure, they can be assured that no malicious actor has been capable of altering the contents of the decrypted message.

To generate a key-pair requires the culmination of several steps, some familiar to prior discussion:

  1. Find two large prime numbers (often selected to be 256-bits in length) $p$ and $q$, which multiplied together equate to $n$ (which will be 512-bits in length assuming both prime numbers were 256-bits in length).
  2. Find some number $e$ that is greater than 1 and less than $(p-1)(q-1)$, and also shares no common factor apart from 1 with $(p-1)(q-1)$ (i.e. such that $e$ and $(p-1)(q-1)$ are co-prime). Many systems choose $e$ to be equal to 3 or 65537, but neither choice is necessarily guaranteed to be valid choices.
  3. The public-key is generated by concatenating $n$ and $e$. From this point the public-key can be shared safely (assuming it is computationally infeasible to factor $p$ and $q$ from $n$ which is why Shor’s Algorithm is a vulnerability).
  4. The private-key is generated by finding $d$ which is equal to 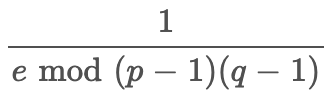$\frac{1}{e \ \mathrm{mod} \ (p-1)(q-1)}$. This key must be kept secret to ensure cryptographic security of the key-pair.

If $n$ can be factorised by a malicious user to find $p$ and $q$ in polynomial time, then $d$ can be calculated in polynomial time and used to forge signatures while posing as the genuine user, or to decrypt messages intended only for the genuine user.

Blockchain mining

The consensus mechanism for many blockchains is Proof-of-Work (PoW), where nodes are required to expend computational resources (i.e. do work) to validate transactions. This generally comes in the form of performing hash operations until a valid hash is obtained. The security of cryptographic hash functions ensure that there is no algorithm to obtain a valid hash more efficiently than guessing (i.e. computing as many hashes as possible and hoping that you land on a valid hash). This process can be sped up using Grover’s algorithm (Section 1.1.2) which enables a quadratic speed up, barring large overheads to implement the specific hash function oracle on a quantum device. This is in fact an area of current research in the quantum computing community. However, assuming this quadratic speed-up is attainable, a node that has access to a quantum device will be able to find valid hashes faster than the classical hardware used today. With only certain individuals and large organisations having access to quantum computers, this may result in centralisation of the blockchain node network to nodes that have access to quantum devices. However, it is yet to be seen whether the Proof of Work model persists with blockchains such as Ethereum looking to fork to a Proof-of-Stake (PoS) consensus mechanism. Hence, with large scale quantum computers predicted to be 10+ years away, mining advantage from quantum computers will most likely not be the primary concern for blockchain protocols.

Post-Quantum Cryptography

Quantum resistance is the term used to describe protocols that are not vulnerable to attacks by quantum computers and are therefore resistant to a quantum future. This has recently become a crucial selling point for those developing security protocols for blockchain. The methods that accommodate quantum resistant algorithms lie within the field of Post-Quantum Cryptography. In this section, we will explore some of the leading contenders for a quantum resistant blockchain. The areas of most interest in this article are Hash-based and Multivariate cryptography; however, we will also have a brief look at Code-based and Lattice-based schemes to address the common researched areas of post-quantum cryptography.

Hash-based cryptography

Interestingly, hash-based cryptographic solutions for sender verification have existed for quite some time. However, it is only after the rapid development of QC have these techniques garnered greater attention. Many of the following exploit known cryptographic hash functions to verify a user with a public-key/private-key style protocol. The one-way nature of hash functions result in what are called One-Time Signatures (OTSs). As the name suggests, an OTS can only be used once, meaning that hash-based authentication requires an additional mechanism for the generation of OTSs. Each additional message that a OTS is used to sign for reduces the security assumptions of said signature (i.e. a malicious actor may be able to forge your signature).

Lamport One Time Signature Scheme

As stated in the name, the Lamport One-Time Signature Scheme (LOTSS) is an OTS that can be constructed with any secure hash function [1]. We describe the scheme in three stages: key generation, signing and verification [2].

Key Generation. Alice who is sending a signed message to Bob must first create a Lamport key pair: the private and public-key. Given a cryptographic hash function $H : [0, \ 1]^* \rightarrow [0, \ 1]^s$ , to sign a message $M \in [0, \ 1]^k$ , where $k$ is a natural number, we choose $2k$ binary integers to form a $2 \times k$ matrix, $K^S_{ij}$, where $0 \leq j < k$ and $i \in [0, \ 1]$. $K^S$ is the private-key with the associated public-key being the hash $K^P_{ij}= H(K^S_{ij})$, computed for all $i$ and $j$.

Signature Generation. To sign the $k$ bit message $M=m_1, \ ..., \ m_k$, we define the signature $S(M) =(K^S_{m_1,0},K^S_{m_2,1}, ..., K^S_{m_k,k-1})$. Remembering that $m_i \in [0, \ 1]$, what we are doing at this point is selecting the corresponding private-key row based on the bit value of the message, i.e. if the $i^{th}$ message bit is $0$, the $i^{th}$ bit of the first row is chosen for the $i^{th}$ bit of the signature. This can understood by expanding the matrices with the following example.

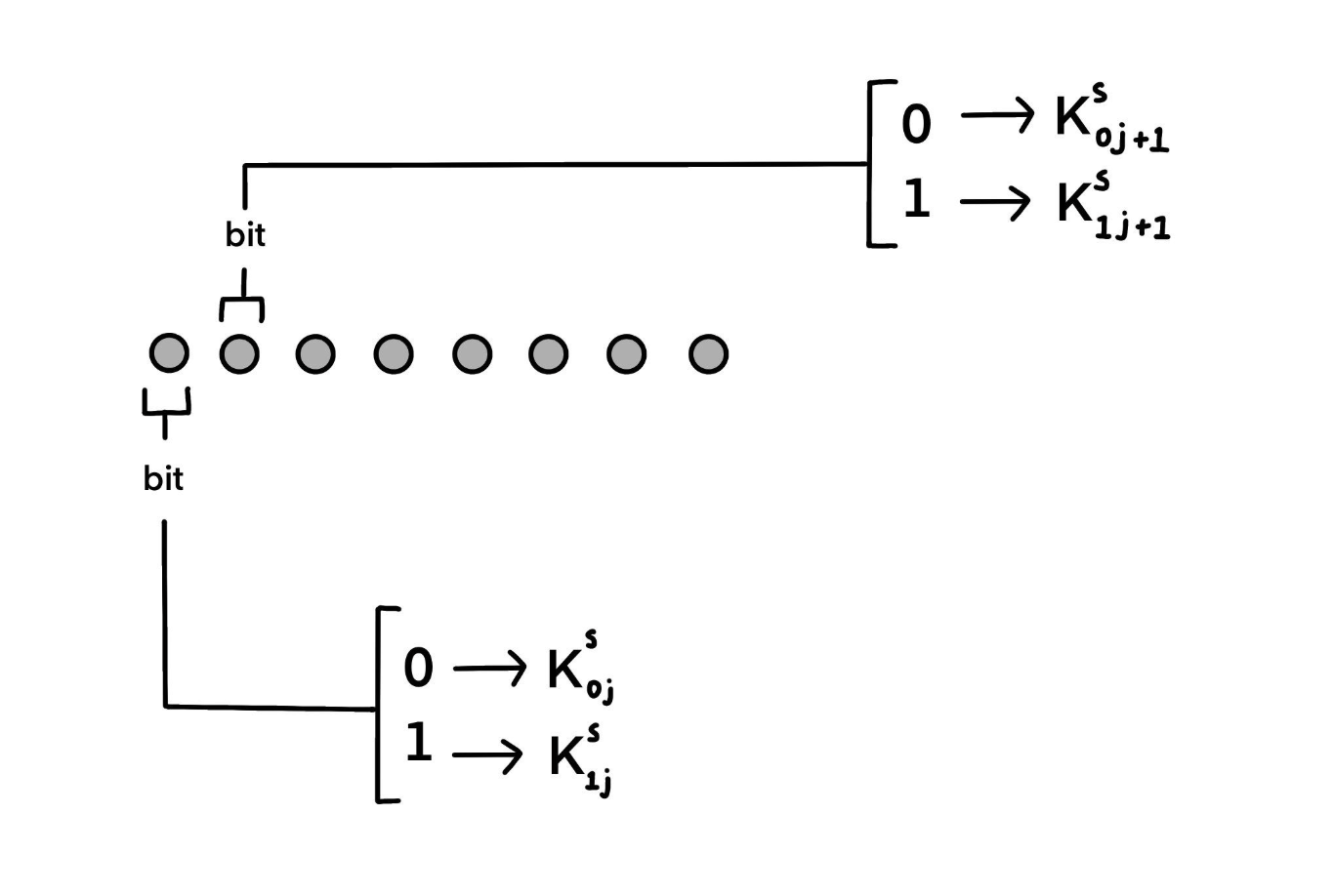
In addition to the message, this signature is sent by Alice. In addition to the message, this signature is sent by Alice.

Signature Verification. To verify that the signature S must have come from Alice, we simply check against the public-key. More specifically we check the following condition, $H(S_i) = K^P_{i, \ m_i}$.

This is one of the more simple hash-based authentication protocols and is also very limited. Every time Alice wants to send a message, she would need to broadcast a new public-key. As is, this method would not be viable for blockchain as the former defines a user by their public-key. Furthermore, the size of the public-key and private-key is a major limitation [1]. This is due to the fact that to achieve a security of $O(2^n)$ a hash function must have at least $2n$ bits. Hence both public-keys and private-keys must at least be of length $2kn$. Since the message is hashed before it is signed, the size of the message is usually $2n$. Therefore, the size of keys are required to be $4kn^2$. Since $n$ is usually required to be greater than $80$ this can become quite large.

Winternitz One Time Signature Scheme

Winternitz One Time Signature Scheme (WOTSS) is an OTS that is able to improve on the size of the public-keys and private-keys at the cost of requiring more hash operations. Again, due to its use of hashing, it is in fact a quantum resistant digital signature. Again an observation of the three stages of key generation, signing and verification is made.

Key generation. Parameter $w\in N$ is chosen and the following is computed, $t=B+\lceil \frac{\lfloor \log_2(B) \rfloor + 1 + w}{w} \rceil$ where $B = \lceil \frac{s}{w} \rceil$ and $s$ is the size of the hash output. The reasoning for this selection is beyond the scope of this article and is not critical to understand WOTSS. One generates $t$ random numbers $x_1, \ ... , \ x_t \in [0, \ 1]^s$ to form the private-key, $K^S = (x_1| \ ...| \ x_t)$. Given a cryptographic hash function $H : [0, 1]^* \rightarrow [0, \ 1]^s$ the public-key $K^P$ is generated by computing $Y_i = H^{2^w} (x_i)$ )i.e. each column of the private-key is hashed $2^w$ times). The public-key is then the concatenation, $K^P=(Y_1| \ ...| \ Y_t)$. In practice, SHA256 is used, which gives $s=256$ and one sets $w=8$ giving $t=32$. Hence, the private-key is a set of 32 256-bit random numbers. Each number is then hashed 256 times to give 32 values forming the public-key.

Signature Generation. Given a hashed message $M = m_1, \ ..., \ m_s$, where $m_i \in [0, \ 1]$, it is split into $B = \lceil \frac{s}{w} \rceil$ number of blocks $b_1, \ ..., \ b_B$ of length $w$ with zero padding if required. The signature is then constructed by taking each $x_{i}$ and applying the hash $2^w-b_i$ times, i.e. $S_i = H^{2^w-b_i}(x_i)$. The signature of the message is then the concatenation $S = (S_1| \ ...| \ S_t)$. Again if we walk through an example, a message is hashed using SHA256 and split in 32 8-bit chucks, $b_1, \ ..., \ b_{32}$. Each, $x_i$, is then hashed $256-b_i$ number of times. Concatenating the outputs then forms the signature.

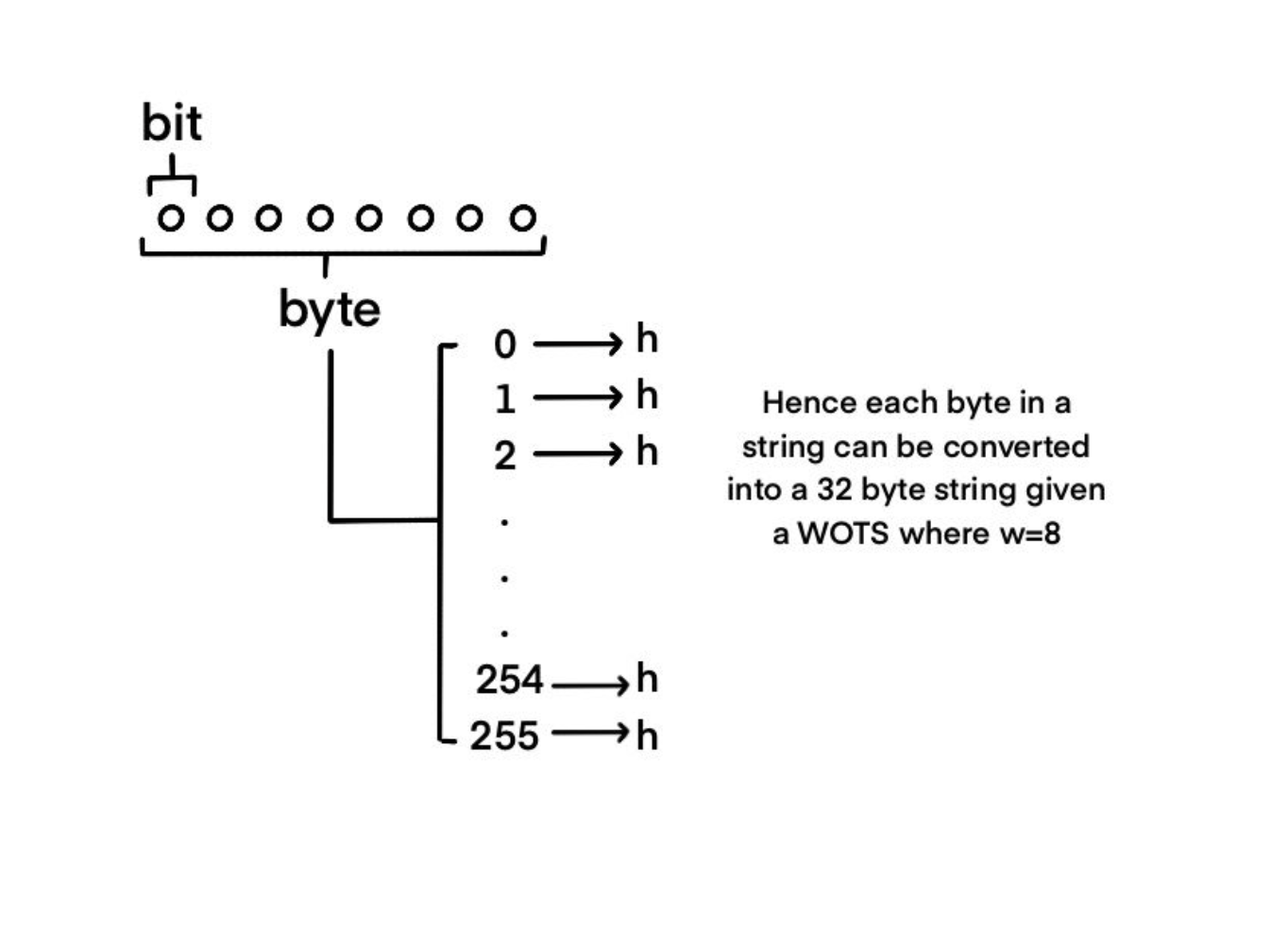In addition to the message, this signature is sent by Alice. In addition to the message, this signature is sent by Alice.

Signature Verification. To verify the message, one takes the signature received $S$ and computes it in a similar manner to derive $S_1, \ ..., \ S_B$ blocks of the signature of length $w$. Each signature column $S_i$ is then hashed a further $b_i$ times. What we should be left with is the public-key, thus concluding the verification.

Generating a WOTS using this described method is vulnerable however without additional actions performed by the generator of the signature. This is a result of the observation that if $b_i$ is equal to $2w-g$ and the user signs this blocks and shares it, any user can read $S_i$ (this is true regardless of the value of $b_i$). In this particular example though where $S_i$ was generated by finding $H^g(x_i)$, a malicious actor could sign any $b_j$ where $b_j$ is less then or equal to $b_i$. There are a multitude of proposed methods to avoid this problem that tend to involve a doubling of signature lengths and/or computations of hashes. None of these methods however are within the scope of this article.

Similar to all hash-based signature schemes, the technique is based on the one-way computation of the hash function. Though this may seem like a great solution, there remains the problem of the public-keys being one time use and signatures being large in size ($sB$ bits per signature). In the next section we will see that the one-time use of public-keys can be overcome by using a Merkle tree.

Merkle Signature Scheme

In most popular blockchain protocols, the public address of the user is the only identifier of a user. Unlike bank accounts in central banking systems where a person is linked to an account, any third party with access to one’s private-key, associated to a public address, is practically just as much the owner of the account with no distinction between person and address. Therefore it is not viable to use OTS schemes for blockchain protocols. However, we can employ ideas from LOTSS and WOTSS to create a system where a single public-key can be used to sign many messages. The Merkle Signature Scheme (MSS) allows us to do exactly this by constructing a Merkel tree with the root as the public-key. It is important to note, though MSS is not an OTS, the number of messages (hence transactions for a blockchain) that can be sent is still finite.

Key generation. The possible number of messages is a power of $2$ due to the binary nature of a Merkle tree. Let $N=2^n$ be the number of possible messages. We now generate $N$ public-key and private-key pairs $[x_i, \ Y_i]_{i=1}^N$ to use as one-time signatures. Either of the OTS schemes in sections 3.1.1 and 3.1.2 can be used. Note, these are not the public-keys for MSS - just for the OTSs. Given a hash function $H : [0, \ 1]^* \rightarrow [0, \ 1]^s$ each $Y_i$ is hashed $h_i=H(Y_i)$ which form the $N$ leaves of a Merkle tree. As seen in the figure below, pairs of child nodes are hashed together to form the parent all the way up to the root of the tree. The root is now broadcasted as the public-key for MSS. The nodes of the tree are labelled as $a[i, \ j]$ where $i$ denotes the level of the node away from the leaves. Hence, $a[0, \ i] = h_i$ and the public-key is $K^P=a[n, \ 0]$.

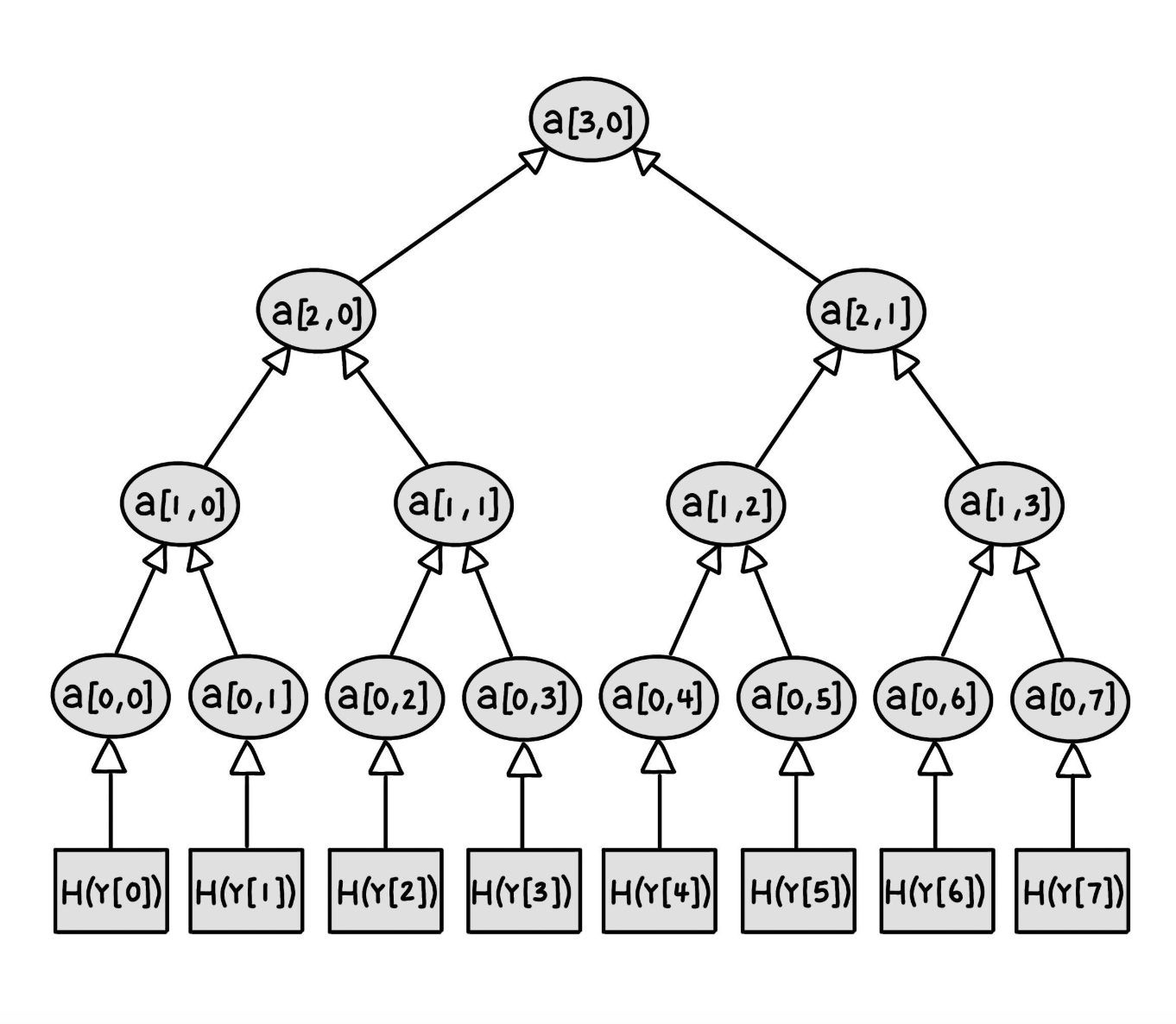Example of the construction of a Merkle Tree, beginning with $8$ private-keys $Y_i$. Example of the construction of a Merkle Tree, beginning with $8$ private-keys $Y_i$.

Signature Generation. Given a message $M$, it is first signed with an OTS scheme using one of the OTS public-key/private-key pairs $(x_i, \ Y_i)$ to construct the signature $S'$. The path is traversed from $a[0, \ i]=h_i=H(Y_i)$ up to the root node, with the traversed nodes listed as $A[0]=a[0, \ i], A[1], \ ... , \ A[n]=K^P$. To compute the hashes required to traverse this path, requires the sibling nodes denoted $auth_0, \ ... , \ auth_{n-1}$ for all $A[0], ... , A[n-1]$ nodes. The final signature of MSS is a tuple $S=(S', Y_i, \ auth_0, \ ... , \ auth_{n-1})$ .

Signature Verification. The verifier is given the following: the message $M$, the signature $S=(S', \ Y, \ auth_0, \ ... , \ auth_{n-1})$, and the public-key $K_P$. The first step is to verify the one-time signature $S'$ is consistent with the message $M$ and the OTS public-key $Y$. Again this is using the OTS schemes from previous sections. Once this has been verified, $auth_0, \ ..., \ auth_{n-1}$ hashes are used to compute up to the root of the tree starting from $H(Y)$. The root computed is then compared with $K_P$ to confirm that they are identical.

MSS allows many more messages with a single public-key at the expense of a larger signature and greater computational effort in producing the tree. Furthermore, we have a finite set of $(x_i, Y_i)$ that can each be used only once. Though one can create a larger tree this requires either a large amount of storage or substantial re-computation if one were to create leaves using a random number generator. MSS inspires further improvements, including the Extended Merkle Signature Scheme (XMSS) [17].

Additional uses of the Merkle Tree

As explained above, Merkle Trees can be used to concatenate many OTS (one-time signatures) together for a single public-key of length $s$ where this denotes the bit-length of the hash function (in the case of SHA256 this is equal to 256) to create a FTS (few-time signature). Merkle Trees however can also be employed directly on a OTS to create a public-key of bit-length $s$ instead of $sB$ in the case of WOTS or $s^2$ in the case of LOTSS. This mechanism is also necessary at a minimum to be able to construct a FTS as described above.

Signature Generation. Assuming that $s=2^j$ where $j \in \mathbb{Z}$ in the case of LOTSS, or that $B=2^j$ in the case of WOTS, each of the public-keys $y_i$ for either of the OTS can be hashed once to create the leaf nodes for a Merkle Tree. As with above each leaf node can be hashed together in pairs of two till a root node $Y$ is generated.

Signature Verification. When a user receives a signature S generated through either of the previously described OTS schemes they will require the additional information of $y_1, \ ..., \ y_n$ public-keys which can be used to verify the public-key $Y$. This action must be performed in addition to their typical verification duties for a given OTS.

Multivariate cryptography

Multivariate cryptography, also referred to as Multivariate Public-Key Cryptography (MPKC), is a protocol whose public-keys are a set of multivariate polynomials. More specifically, the trapdoor one-way function is usually a multivariate quadratic polynomial map over a finite field and is therefore referred to as multivariate quadratics. The method is predicated on the hardness (NP-hard) of solving a set of quadratic equations over a finite field. Inverting a multivariate quadratic map is equivalent to solving a set of quadratic equations $p_1, ... , p_m \in \mathbb{R}^{\mathbb{R}^n}$ over a finite field, known as the MQ problem.

MQ problem. Solve $p_1(x)=p_2(x)= ... = p_m(x)=0$, where $p_i$ are quadratic maps on $x \in \mathbb{R}^n$ and all coefficients are over some finite field.

This will be clearer as how the protocol works is explored. However, the most critical characteristic is that Shor’s algorithm cannot be used to break this MQ problem. The public-key is given by a set of polynomial functions that is assumed to be polynomial from this point onwards.

$$ \begin{align*} P(x_1, \ ..., \ x_n) &=p_1(x_1, \ ..., \ x_n), ..., p_m(x_1, \ ..., \ x_n) \\ p_k&= \sum_{i=1}^n \sum_{j=1}^n R_{ijk}x_i x_j + \sum_{i=1}^n Q_{ik} x_i \end{align*} $$

Known as tensors, $R_{ijk}$ and $Q_{ik}$ store the characteristics of the polynomial for all $p_k$. All coefficients and variables lie in a finite field $\mathbb{F}_q$ of $q$ elements. It will be seen that computing these polynomials at given values correspond to both the encryption and verification stages. Crucially, this public polynomial is a composition of a private central map $Q$ that is hidden using two random full-rank affine maps, $[U, \ V]$. The public-key has the form, $P=U \circ Q \circ V=U(Q(V(.)))$, more specifically, given $Q=(q_1, \ ..., \ q_m)$ the public polynomial has the following form.

$$ \begin{equation*} P(x) =(p_1, ... ,p_m) (x) = U(q_1[V(x)], ... , q_m[V(x)]) \end{equation*} $$

The scheme is constructed such that the hidden central map is easy to solve, hence allowing $P$ to be easily solved by any actor who knows $[U, \ V, \ Q]$. One should note, affine transformations are easy to invert as it is a problem of inverting a square matrix for which there exists a tractable solution. There are families of multivariate schemes giving several choices for the map $Q$, some of which can be found in [5]. Importantly, some schemes have been broken. Encryption works in the following way given a message in plaintext $M=(x_1, ... , x_n)$ the ciphertext is a simple polynomial evaluation given below. For one to be able to decrypt the message from the ciphertext, they would need to know the inverse map $P^{-1}$ which is not practical to solve without knowing the hidden private-keys $U,V,Q$.

$$ \begin{align*} P(M) &= p_1(x_1, ..., x_n), ..., p_m(x_1, ..., x_n)=(c_1, ... ,c_m) \\ P^{-1}(c_1, \ ..., \ c_m)&=(x_1, \ ..., \ x_m)=V^{-1} \circ Q^{-1} \circ U^{-1}(c_1, \ ..., \ c_m) \end{align*} $$

Key Generation. This is the generation of two random full-rank affine maps, $U,V$ as well as a easy to invert $Q$ from a MPKC scheme.

Signature Generation. Given a hash, $h_1, ... , h_m$ of a message, Alice signs the message by computing the following signature.

$$ \begin{equation*} S=(x_1, ... , x_m) = P^{-1}(h_1, ... , h_m) \end{equation*} $$

Signature Verification. To verify the signature one simply needs to ensure the following holds true.

$$ \begin{equation*} (h_1, ... , h_m) =P(x_1, ... , x_m) \end{equation*} $$

A disadvantage of MPKCs are the often large keys required when compared against RSA or ECC. For example, RSA-2048 requires not much more than 2048 bits while the Rainbow signature scheme, a MPKC scheme, has a public-key size of 181440 bits [6]. Another drawback of MPKCs is the fact that they often do not have provable security results, as they are only resistant to known attacks.

Code-based cryptography

Code-based cryptosystems are another family of PKCs that employ error correcting codes to construct the crucial one-way function. In this section we will explore the first code-based public-key/private-key encryption scheme proposed by McEliece [7], often referred to as the McEliece Cryptosystem. However, to understand how it works, we will give a short introduction to error correcting codes, more specifically the linear Goppa codes.

Error correcting codes (ECCs) were initially constructed for communicating across noisy channels. These codes are constructed by adding redundant information that ensures that a limited number of errors can be corrected by exploiting the added information. For example, the simplest ECC is the repetition code. Say Alice wants to send Bob a bit of information, the bit is repeated three times and either 000 or 111 is sent across the channel. Assuming the channel is noisy and some bits may be flipped, Bob may receive any of the following messages.

Message Received Correct to Interpreted as
000 (no error) 000 0
001 000 0
010 000 0
100 000 0
011 111 1
110 111 1
101 111 1
111 (no error) 111 1

It is seen that a single error (a single bit flip) does not alter the message. Hence it is possible to correct for errors. It is important to observe that this particular ECC cannot correct for more than a single error. For example, a 000 message with two errors giving 011 will be corrected to 111 which is in fact incorrect. Now that we have an understanding of ECCs, we define a family of ECCs, referred to as linear codes, which contain additional structure.

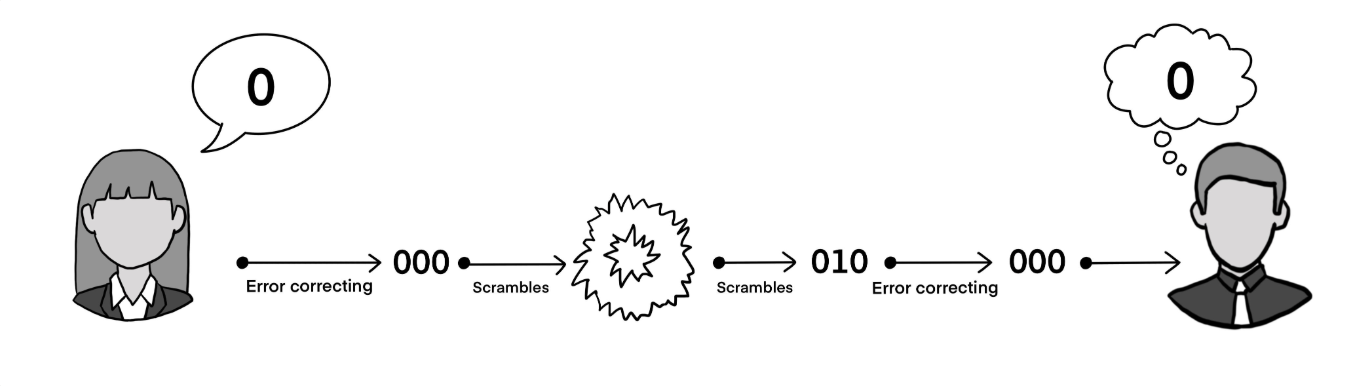
Example of an Error Correcting Code for a message from Alice to Bob. Example of an Error Correcting Code for a message from Alice to Bob.

Linear codes (LCs) A linear code of dimension $k$ and length $n$ over a finite field $\mathbb{F}$ is a $k$ dimensional subspace of the vector space $\mathbb{F}_n$. Such a linear code can be referred to as an $[n, \ k]$ code. Given the minimum Hamming distance between codewords is $d$, it is also referred to as an $[n, \ k, \ d]$ code. A crucial property of LCs is that any linear combination of codewords is also a codeword. In order to understand Goppa codes a Goppa polynomial must first be defined.

Goppa polynomial. Let a Goppa polynomial be defined as a polynomial over a finite field (also known as a Galois field), $GF(p^m)$, where $p$ is a prime number and $m$ is an integer greater than $1$ of the below form where $g_0, \ g_1, \ ..., \ g_t \in GF(p^m)$.

$$ \begin{equation*} G(x)=g_0+g_1x +g_2x^2+ ... + g_tx^t= \sum_{i=0}^t g_i x^i \end{equation*} $$

Goppa Codes (GCs)

Goppa codes are linear ECCs that uses Goppa polynomials to encrypt and decrypt messages. Letting L be a finite subset of $GF(p^m)$ such that $G(\alpha_i) \neq 0$ for all $\alpha_i \in L$ a codeword $c=(c_1, ... , c_n)$ can be defined to construct $R_c(x)$.

$$ \begin{align*} L &= [\alpha_1, \ \alpha_2, \ ..., \ \alpha_n] \subseteq GF(p^m) \\ R_c(x) &= \sum_{i=1}^n \frac{c_i}{x-\alpha_i} \end{align*} $$

Given the above, $\frac{1}{x-\alpha_i}$ is defined as the polynomial that satisfies $\frac{1}{x-\alpha_i} \cdot(x-\alpha_i) =1 \ \mathrm{mod} \ g(x)$. The Goppa code $\Gamma(L, \ g(x))$ is then defined as the set of codewords $c$ that satisfy $R_c(x) = 0 \ \mathrm{mod} \ g(x)$. In other words, $g(x)$ divides $R_c(x)$. For cryptography, one uses a binary irreducible Goppa code, where the polynomial is over field $GF(2^m)$. Here irreducible implies that $d \geq 2t+1$, where $d$ is the code distance and $t$ is the degree of the Goppa polynomial. Finally a generator matrix that is used for the encryption of messages is defined.

Generator Matrix. The generator matrix of a $[n, \ k]$ Goppa Code is defined to be the $k\times n$ matrix $G$, where the rows of $G$ form the basis of the Goppa Code $\Gamma(L, \ g(x))$.

Error correction for Goppa codes are performed using Patterson’s algorithm for errors less than $t$. An explanation of Patterson's algorithm is beyond the summary that we attempt to provide in this article, however further information can be found in [8,9].

McEliece Cryptosystem

The McEliece Cryptosystem uses binary irreducible Goppa codes to create a public-key and private-key protocol for authenticating messages based on the hardness of decoding a linear code. Once the main principles of encryption and decryption are understood it is possible to understand the McEliece Digital Scheme. As usual the first step is to generate a key.

Key Generation. An arbitrary $t$-degree Goppa polynomial over $GF(2^m)$ is chosen. The generator matrix $G$ for this Goppa code is then computed. Further, a $k \times k$ invertible matrix $S$ and an $n \times n$ invertible permutation matrix $P$ are randomly selected. The matrix $G'=SGP$ is then made public as well as the degree $t$ of the polynomial whereas $[g(x), \ S, \ G, \ P]$ remain private.

Encryption. To encrypt a message $m=(m_1, \ ..., \ m_k)$, one creates a random binary vector $e$ of length $k$ and computes $y=mG'+e$ which is sent as the ciphertext.

Decryption. The ciphertext can be decrypted by first using the private permutation matrix $P$, where $e':=eP^{-1}$. By applying Patterson’s algorithm, the error $e'$ can be found, allowing for the deriving of $mSG$. Hence, knowing $S$ and $G$ the original message can therefore be decrypted.

$$ \begin{equation*} y'=yP^{-1} =mG'P^{-1}+eP^{-1}=m(SGP)P^{-1}+eP^{-1}=mSG+e' \end{equation*} $$

Digital Signature Scheme

A signature scheme for code-based cryptosystems is much more difficult as one cannot sign by decrypting a hashed message as if it was a ciphertext, with verification being the encryption. This fails, as decryption involves fixing errors while encryption introduces random errors. It is for this reason code-based cryptosystems are often seen as impractical for signature schemes. However, one promising solution was proposed in [8], known as the CFS signature, named after the authors Courtois, Finiasz and Sendrier. The main idea behind this scheme is to hash the message repeatedly until the output becomes a ciphertext that can be decrypted. The signer is then able to compute the corresponding error vector, $e$. The number of times hashed, $n_h$ and the error vector together form the signature, $S=(e, n_h)$. Though the signature can be verified quite easily by hashing the message multiple times and adding the error vector, it is impractical to compute the error vector, and therefore the signature, without the private-key.

Lattice-based cryptography

The use of a lattice for cryptography was first discovered by [4] and is based on the hardness of lattice problems. Lattice-based cryptography (LC) is quite unique to the other forms of cryptography expressed in the article. Where others rely on problems which are hard to solve on average, some lattice problems have strong security proofs based on worst-case hardness. This is one of the reasons, there have been a large number of research publications relating to LC. Furthermore, it is only conjectured that there exist no polynomial time quantum algorithms that can approximate lattice problems. This is despite the fact the Fourier transform is highly relevant to lattice systems and very efficient to calculate on quantum computers. Nonetheless, there are two types of LC schemes that exist today, those that are practical but without proof of security and those that have strong security guarantees but are somewhat inefficient. The latter remains more promising and will be discussed further in this section. However, first a small introduction to lattices and the lattice problems most commonly employed in cryptography.

A lattice is a set of points in an $n$-dimensional space that has an underlying periodic structure. This structure is mathematically expressed in terms of $n$ linearly independent vectors $b_1, \ ..., \ b_n \in \mathbb{R}^n$, that form a basis for the particular lattice. Therefore the lattice generated by these vectors have the following form.

$$ \begin{equation*} L(b_1, \ ..., \ b_n) = [\sum_{i=1}^n \alpha_i b_i : \alpha_i \in Z] \end{equation*} $$

Crucially, a lattice does not have a unique basis, meaning that a different set of vectors $[b'_1, \ ..., \ b_n']$ can be employed to generate the same lattice points $L(b_1, \ ..., \ b_n)=L(b'_1, \ ..., \ b'_n)$. A basis can be either called short or long depending on whether the vectors that constitute the basis are small or large, respectively. This distinction becomes essential when attempting to solve various lattice problems. Two of the most common lattice problems seen in the field of cryptography are the Shortest Vector Problem and the Closest Vector Problem.

Shortest Vector Problem (SVP). Given a basis set $[b_1, \ ..., \ b_n]$ and a norm, $||\cdot||$, on the vector space, $V$, find the shortest vector in the lattice $L(b_1, \ ..., \ b_n)$.

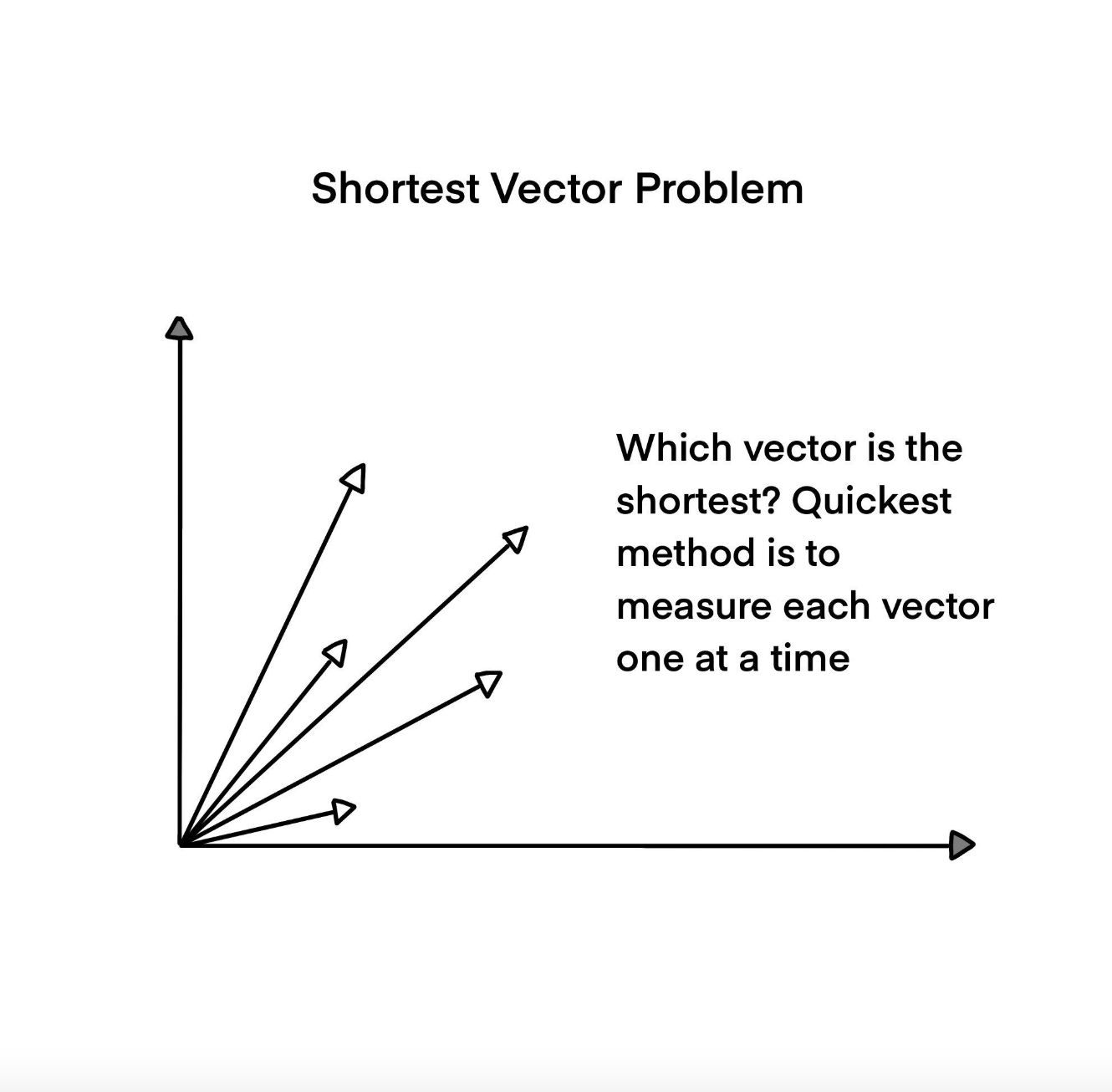Visualisation of the Shortest Vector Problem. Visualisation of the Shortest Vector Problem.

Closest Vector Problem (CVP). Given a long basis $b^L_1, \ ..., \ b^L_n$ for a lattice $L(b^L_1, \ ..., \ b^L_n)$ and randomly chosen point $P$, find the closest point in $L$ to $P$.

It turns out that both SVP and CVP are quite easy to solve if a short basis is given. This is a common characteristic of many lattice problems, which essentially allows for a trapdoor that can be exploited in cryptography. This brings forth one of the most straightforward public-key/private-key signature schemes based on lattices, the GGH signature scheme.

GGH Signature Scheme

This system was proposed by Goldreich, Goldwasser, and Halevi [20] and is similar to the McEliece cryptosystem we described earlier in Section 3.3. The system is based on the hardness of CVP in a lattice, with the trapdoor being a short basis for the lattice.

=Key Generation. Private-key is defined as a good lattice basis $B$, both short and almost orthogonal, for a lattice $L(B)$. The public-key, $H$, is a long basis for the same lattice and is generally far from orthogonal. Mathematically the public-key and private-key satisfy the condition $L(B)=L(H)$.

Signature Generation. Given a hash, $h \in \mathbb{R}^n$, of a message, the signature is generated by rounding $h$ to the nearest lattice point, $S\in L$ using the secret good basis. This can be done efficiently using Babai’s rounding off procedure [21]. S is sent as the signature.

Signature Verification. Verification can be carried out by first checking that $S\in L$ using the public basis keys. Secondly, one would need to check that $|S-h|$ is small, where $h$ is the hash of the message supplied.

Forging a signature without the secret good basis is analogous to solving CVP and is therefore a hard problem. Though it has been shown there are vulnerabilities to this scheme, as each signature leaks information about the private-key, there are perturbation techniques to extend GHH and get around this problem. Techniques such as the NTRUSign signature scheme have shown great promise in this area.

Quantum cryptography

Finally, we get to an area of cryptography that many have never heard, the field of quantum cryptography. The same technology that can disrupt most encryption protocols today, also provides a solution. Though we gave an introduction to Quantum Computing, it is not possible to explain in fine detail the inner workings of quantum cryptography. Rather, we will give an overview, with the reader getting an idea of how this form of cryptography operates.

We look at the most basic protocol for a quantum digital signature, known as the Gottesman-Chuang quantum signature scheme [14], a one-time signature scheme. As usual, we will look at the three stages independently: key generation, signature generation and signature verification [15].

Key Generation. The protocol initially assumes that all participants know a particular mapping from bit string to quantum state $F:k \rightarrow |f_k>$, and security parameters $c, \ j$. The brackets $|\cdot>$ indicate that we have a quantum state. Alice chooses random $L$-bit strings $[k^i_0, \ k^i_1, \ 1\leq i \geq j]$. These form Alice’s private-keys with their associated quantum maps $|f_{k_0}>, \ |f_{k_1}>$ forming the public-keys. Important to note, the public-keys are quantum states. Due to the nature of quantum mechanics, these public-keys can only be generated by Alice efficiently, and cannot be cloned.

Signature Generation. Similar to Lamport’s scheme, to sign a bit $b$, Alice generates $(b, \ k^1_b, \ k^2_b, \ ..., \ k^j_b)$ and sends it to Bob. Therefore Alice reveals half of her public-keys and subsequently discards all used and unused private-keys.

Signature Verification. The verifier simply checks whether the mapped state $k^i_b \rightarrow |f_{k^i_b}>$ matches its associated public-key. This is because it turns out to be relatively easy to check whether two quantum states are similar without knowing much about either state. The number of correct keys $s$ is counted and the signature is accepted if $s\leq cj$ is satisfied.

This scheme relies on the fact that quantum states are not able to be copied, which is due to what is known as the no cloning theorem. Since a quantum public-key cannot be copied, one may try to reconstruct it. However, this is not only exponentially hard in terms of time-complexity, it is also infeasible to store in memory. A 60 qubit system will require roughly 4 million terabytes of classical storage. Nonetheless, it is clear this method is highly inefficient, especially as one would require a quantum channel to communicate with quantum states. Therefore the main idea for this section was to illustrate the principles behind a signature scheme that employs quantum physics.

Appendix

Appendix A: Mathematical Groups

In mathematics, a group is a particular structure given to a set with the addition of a binary operation that takes two elements from the set and returns another element also in the set. Given a set $S$ and binary operation $\cdot$, it can be said that $(S, \ \cdot)$ forms a group if the following group axioms are satisfied. It should be noted that in the discussion of groups formed from elliptic curves, the notation $+$ is used for the binary operation. This is simply different for the binary operation.

$$ \begin{align*} &\mathrm{(Associativity)} \ a\cdot(b\cdot c)=(a\cdot b)\cdot c, \ \forall a, \ b, \ c \in S \\ &\mathrm{(Existence \ of\ identity \ element)} \ \exists I\in S : I\cdot a=a, \ \forall a \in S \\ &\mathrm{(Existence \ of \ inverse \ element)} \ \forall a \in S, \ \exists b \in S : a\cdot b=b\cdot a=I$ \end{align*} $$

Appendix B: Mathematical proof of ECDSA

The reasoning for many of the steps in ECDSA, as explained in Section 2.1.1, may not have been quite obvious. Here, we walk through the mathematics to explain exactly how the algorithm works [18].

We start with an explanation of signature verification which will elucidate the reasoning for why the particular signature was made. The verifier (Bob) computes $P=uB+vK^P$ where $u=s^{-1} z \ \mathrm{mod} \ r$ and $v=s^{-1}d \ \mathrm{mod} \ r$ are also computed. The public-key $K^P$ and the base point $B$ are known to all. Recall that the public-key is defined as $K^P=K^S B \ \mathrm{mod} \ p$ where $K^S$ is the private-key. Putting all these equations together (leaving out $\mathrm{mod} \ r$) the following is found.

$$ \begin{align*} P&=uB+vK^P \\ P&=uB+vK^SB \\ P&=s^{-1}(z+dK^S)B \\ P&=kB \end{align*} $$

This is precisely how Alice generated the signature in the first place. Hence, by verifying $d=x_P \ \mathrm{mod} \ r$ (where $x_P$ is the $x$-coordinate of $P$) with $d$ given by Alice as part of her signature, we can confirm that the signature must have come from Alice.

References

[1] Becker, G., Merkle signature schemes, merkle trees and their cryptanalysis. Ruhr-University Bochum, Tech. Rep (2008).

[2] Chang, M.-H. & Yeh, Y.-S. Improving Lamport one-time signature scheme. Appl Math Comput 167, 118–124 (2005).

[3] Corporation, I., 2022. Math Paths to Quantum-safe Security: Hash-based Cryptography - ISARA Corporation [online] ISARA Corporation. Available at: https://www.isara.com/blog-posts/hash-based-cryptography.html

[4] M. Ajtai. Generating hard instances of lattice problems. In Complexity of computations and proofs, volume 13 of Quad. Mat., pages 1–32. Dept. Math., Seconda Univ. Napoli, Caserta, 2004. Preliminary version in STOC 1996

[5] Louis Goubin, Jacques Patarin, Bo-Yin Yang, Multivariate Cryptography

[6] Jintai Ding and Bo-Yin Yang, Multivariate Public Key Cryptography

[7] McEliece, R.: A public key cryptosystem based on algebraic coding theory. DSN progress report, 42-44:114–116 (1978).

[8] Nicolas Courtois, Matthieu Finiasz, and Nicolas Sendrier, How to achieve a McEliece-based Digital Signature Scheme

[9] S. V. Bezzateev and I. K. Noskov, "Patterson Algorithm for Decoding Separable Binary Goppa Codes," 2019 Wave Electronics and its Application in Information and Telecommunication Systems (WECONF), 2019, pp. 1-5, doi: 10.1109/WECONF.2019.8840650.

[10] Image Ref: https://medium.com/@peterreid_12788/part-2-is-elliptic-curve-cryptography-ecc-a-step-towards-something-more-understanding-ecc-3c933d3922e

[11] Wikimedia Foundation. (2022, January 25). Group (mathematics). Wikipedia. Retrieved February 3, 2022, from https://en.wikipedia.org/wiki/Group_(mathematics)

[12] Shor, P.W. (1994). "Algorithms for quantum computation: discrete logarithms and factoring". Proceedings 35th Annual Symposium on Foundations of Computer Science. IEEE Comput. Soc. Press: 124–134

[13] Gidney, C. & Ekerå, M. How to factor 2048 bit RSA integers in 8 hours using 20 million noisy qubits. Quantum 5, 433 (2021).

[14] D. Gottesman and I. Chuang, Quantum Digital Signatures. arXiv:quant-ph-0105032 (2001).

[15] Zhengjun Cao, A Note On Gottesman-Chuang Quantum Signature Scheme, eprint.iacr.org/2010/317

[16] Peter Waterland, (2016), https://www.theqrl.org

[17] A. Huelsing, TU Eindhoven, D. Butin, TU Darmstadt, XMSS: eXtended Merkle Signature Scheme (2018)

[18] Andrea.corbellini.name. 2022. Elliptic Curve Cryptography: ECDH and ECDSA - Andrea Corbellini. [online] Available at: https://andrea.corbellini.name/2015/05/30/elliptic-curve-cryptography-ecdh-and-ecdsa/

[19] Zcash: Internet Money, GitHub, Available at: https://github.com/zcash/zcash

[20] Oded Goldreich, Shafi Goldwasser, and Shai Halevi. Public-key cryptosystems from lattice reduction problems. In Burton S. Kaliski, editor, Advances in Cryptology – CRYPTO ’97, volume 1294 of LNCS, 1997

[21] Babai, L.: On Lovász lattice reduction and the nearest lattice point problem. Combinatorica, 6:1–13 (1986)

This document was authored by Maiyuren Srikumar during his internship.